lucky site

精于心，简于形

文章目录 站点概览

lucky luser

人生是旷野

15 文章
7 标签

Pruning[NISP'15] paper code reproduction

发布于 2023-02-22 | 标签: AI 、 TinyML | 15分钟 | 2906字数

Created: February 22, 2023 8:37 PM
Created by: Luser
Type: AI、model compression

使用基于numpy构建的全连接层神经网络来对这篇paper进行简单的实验复现，源码： Github

Pseudo-code

Untitled

Code implementation

Make mask matrix and pruning

Set threshold

对任意矩阵，设置一个threshold，矩阵中小于这个threshold的元素就置为0(False)，大于threshold的元素置为1(True)，这样就得到了这个矩阵的mask矩阵

  • code

    import numpy as np
a = np.array([[0,1,2,3,4],[5,6,7,8,9]])
threshold = 4
print("oriarray:")
print(a)
mask = a > threshold
a=np.multiply(a,mask)
print("pruning:")
print(a)

  • output

    oriarray:
[[0 1 2 3 4]
 [5 6 7 8 9]]
pruning:
[[0 0 0 0 0]
 [5 6 7 8 9]]

对于未知、元素量大的矩阵，想要获得其mask矩阵，使用下面这个函数

np.percentile(arrary, number)

这个函数将矩阵内的元素从小到大排列并且按照 number 索引去取得相应的分位数，number是0~100的数，比如number=50，就会将矩阵里所有

元素分为等量的两份，返回两份数字之间的中位数。number=1，就会将矩阵分为1:99的两份数，返回这两分数之间的数。也就是返回按比例分组

的阈值。

所以可以改进上面生成mask矩阵的代码：

  • code

    import numpy as np
a = np.array([[0,1,2,3,4],[5,6,7,8,9]])
h_threshold = 20
print("oriarray:")
print(a)
threshold = np.percentile(a, h_threshold)
mask = a > threshold
a=np.multiply(a,mask)
print("pruning:")
print(a)

  • output

    oriarray:
[[0 1 2 3 4]
 [5 6 7 8 9]]
pruning:
[[0 0 2 3 4]
 [5 6 7 8 9]]

Continuous pruning

想要对矩阵进行连续的pruning，需要注意np.percentile(a, h_threshold)函数在对元素进行排列时，将所有的0都加入排列了，需要消除0对计算阈值的影响

比如，对于矩阵

[0123456789]\begin{bmatrix} 0&1&2&3&4\\ 5&6&7&8&9 \end{bmatrix}

，如果对它进行20%的pruning，则会得到

[0023456789]\begin{bmatrix} 0&0&2&3&4\\ 5&6&7&8&9 \end{bmatrix}

，但如果继续用原来的方法直接计算阈值对新生成的矩阵

进行20%的pruning，矩阵的值并不会发生变化，原因就是两个0都被放进了数组里进行计算，10个数里的20%自然就是取前两个，也就是前两个0被置为0，

结果也就不变。

为此可以定义一个函数，每次进行连续的pruning时，该函数都将矩阵中的N个0变成一个0，然后再将其余的数添加到对应数组中，也就是这个函数返回的

是只有1个0和输入向量其余非0数的数组：

  • function：

    def array0(a):
	b=[]
	b.append(0)
	for i in a:
		for j in i:
			if j != 0:
				b.append(j)
	return b

  • code:

    #make mask
import numpy as np
a = np.array([[0,1,2,3,4],[5,6,7,8,9]])
print("oriarray:")
print(a)

mask = a > np.percentile(a, 20)
print(np.percentile(a,20))
a=np.multiply(a,mask)
print("pruning:")
print(a)
#直接继续进行20%的pruning，输出不变
mask = a > np.percentile(a, 20)
print(np.percentile(a,20))
a=np.multiply(a,mask)
print("pruning:")
print(a)

def array0(a):
	b=[]
	b.append(0)
	for i in a:
		for j in i:
			if j != 0:
				b.append(j)
	return b
#减去0后连续九次进行20%pruning
b=array0(a)
for l in range(9):
	mask = a > np.percentile(b, 20)
	a=np.multiply(a,mask)
	b=array0(a)

print("pruning:")
print(a)

  • output

    oriarray:
[[0 1 2 3 4]
 [5 6 7 8 9]]
1.8
pruning:
[[0 0 2 3 4]
 [5 6 7 8 9]]
1.6
pruning:
[[0 0 2 3 4]
 [5 6 7 8 9]]
pruning:
[[0 0 0 0 0]
 [0 6 7 8 9]]

Retrain the trained network parameters

这里使用最基础的numpy构建神经网络，该网络可以自定义网络层数和相应节点数，

对一个全连接层的神经网络进行参数pruning复现一下论文里的方法，下面是训练时的神经网络的隐藏层和输出层的结构示意图：

#指定的网络层数和节点数
layer_dims = [train_set_x.shape[0], 5, 4, 3, 2, 1]
https://s2.loli.net/2023/01/03/UjsCw54YH9p2JlT.jpg

这是一个简单的MLP，作用是判断输入的图片中有没有车，如果图片里有车就输出1，图片里没有车就输出0。

通过该网络训练好参数后将其保存下来，后期可以直接加载保存好的参数文件进行预测或者进行再训练。

导入需要的包

from tqdm import tqdm
import numpy as np
import matplotlib.pyplot as plt
from nn_functions import *

载入数据集

##load dataset
datas = 'datasets/carvnocar.h5'
train_set_x, train_y, test_set_x, test_y = load_files(datas)
#行标准化
train_x = train_set_x / 255
test_x = test_set_x / 255

载入参数文件，得到训练好的原始参数和隐藏层层数

##load parameters
f_parameters = 'datasets/parameters.npy'
parameters = np.load(f_parameters, allow_pickle='TRUE').item()
L = len(parameters)//2 #隐藏层层数

编写判断当前参数对输入数据进行预测的准确度的函数

#Print accuracy
def accuracy(parameters):
	Y_prediction_train = predict(parameters, train_x)
	Y_prediction_test = predict(parameters, test_x)
	print("Training set accuracy："  , format(100 - np.mean(np.abs(Y_prediction_train - train_y)) * 100) ,"%")
	print("Test set accuracy："  , format(100 - np.mean(np.abs(Y_prediction_test - test_y)) * 100) ,"%")

由于在retrain-pruning的过程对比之前网络训练的过程中多了一个pruning的过程，

所以不能直接调用之前训练网络参数的函数，需要重写前向传播函数和训练函数：

编写pruning函数：

#pruning function
def prun(parameters, mask_w):
	for l in range(1,L):
		X = parameters['W'+str(l)]
		X = np.multiply(X, mask_w[l-1])
		parameters['W'+str(l)] = X
	return parameters

重写forward函数，编写retrain函数： retrain函数通过调用tqdm包里的功能来实现打印训练过程进度条和实时刷新打印cost值

#Rewrite forward propagation function
def forward_f(X, parameters):
    A = X
    caches = []
    for l in range(1, L):
        A_l = A
        A, cache = forward.activation_forward(A_l, parameters['W'+str(l)], parameters['b'+str(l)], "relu")
        caches.append(cache)
    
    AL, cache = forward.activation_forward(A, parameters['W' + str(L)], parameters['b' + str(L)], "sigmoid")
    caches.append(cache)

    return AL, caches

#Retrain function
def retrain(parameters, X, Y, learning_rate, num_iterations):
	with tqdm(total=num_iterations) as t:
		for i in range(0, num_iterations):
			AL, caches = forward_f(X, parameters)
			cost = np.squeeze(forward.cost_function(AL, Y))
			grads = backward.backward_function(AL, Y, caches)
			parameters = update_parameters(parameters, grads, learning_rate)
			parameters = prun(parameters, mask_w)
			t.set_description('Retrain %i' % i)
			t.set_postfix(cost=cost)
			t.update(1)

	return parameters, cost

重新载入一份参数以此进行pruning，从对伪代码进行复现

prun_parameter = np.load(f_parameters, allow_pickle='TRUE').item()
#hyper-parameters
h_threshold=5
delta=0.1
learning_rate=0.05
num_iterations=220

degrees=[]
costs=[]
for i in range(1, 40):
	#Make mask
	mask_w=[]
	for l in range(1,L):
		a=prun_parameter['W'+str(l)]
		b=array0(a)
		threshold=np.percentile(np.abs(b), h_threshold)
		ms=np.abs(a)>threshold
		if i>1:
			ms=np.multiply(ms,mask_w_l[l-1])# Multiply by the mask matrix of the previous step
		mask_w.append(ms)
		# print("threshold "+str(l)+": "+str(threshold))# print threshold
	mask_w_l=mask_w# Save the mask matrix of the previous step
	#Pruning parameters
	prun_parameter=prun(prun_parameter, mask_w)#parameters pruning
	print("\n "+str(i)+" Pruning parameters: ")
	n=degree(prun_parameter)
	degrees.append(n)
	accuracy(prun_parameter)
	#Retrain parameters
	retrain_parameters, cost = retrain(prun_parameter, train_x, train_y, learning_rate, num_iterations)
	costs.append(cost)
	print("\nPruning and retrain parameters: ")
	accuracy(retrain_parameters)
	np.save('datasets/prun_parameter_1/prun_parameters'+str(i)+'.npy', retrain_parameters)
	#Iterative pruning (Not used during the experiment)
    # h_threshold+=delta*i
	# h_threshold+=5

degree_costs={'degree':degrees,'costs':costs}
np.save('datasets/degree_costs.npy', degree_costs)

这里虽然设置了超参数delta(δ)但是因为用来测试的网络模型很小，禁不起步进比较大的pruning，

就并没有运用到它，而是采用的每次都裁剪同样比例参数的做法层层递进。

Some problems

  1. 对输入进行连续剪枝的时候需要注意到矩阵里 0 的增多造成的影响

    • 通过对上一次mask后的矩阵进行“消零”的处理就可以去除0对mask的影响，

      但引发的新的问题是，我连续剪枝后的矩阵对原矩阵来说并不是每一次都是同样

      的剪枝度，也就是说真实的剪枝度并不是简单的叠加的关系

  2. 连续递进剪枝度进行剪枝的时候，每一次不同程度的剪枝得到的mask矩阵都是相同的，

    也就是说上一次剪枝后被置为0的数由于这一次的mask矩阵是不同的就会有一些0会在Retrain的过程中

    被重新训练回去，这相当于白忙一场

    • 只要在这一次剪枝生成mask矩阵的过程中让这一次的mask矩阵和上一次的mask矩阵按元素相乘，

      得到的这个新的mask矩阵取为本次的矩阵就可以解决这个问题。

Complete Code

from tqdm import tqdm
import numpy as np
import matplotlib.pyplot as plt
from nn_functions import *

#pruning function
def prun(parameters, mask_w):
	for l in range(1,L):
		X = parameters['W'+str(l)]
		X = np.multiply(X, mask_w[l-1])
		parameters['W'+str(l)] = X
	return parameters

#Rewrite forward propagation function
def forward_f(X, parameters):
    A = X
    caches = []
    for l in range(1, L):
        A_l = A
        A, cache = forward.activation_forward(A_l, parameters['W'+str(l)], parameters['b'+str(l)], "relu")
        caches.append(cache)
    
    AL, cache = forward.activation_forward(A, parameters['W' + str(L)], parameters['b' + str(L)], "sigmoid")
    caches.append(cache)

    return AL, caches

#Retrain function
def retrain(parameters, X, Y, learning_rate, num_iterations):
	with tqdm(total=num_iterations) as t:
		for i in range(0, num_iterations):
			AL, caches = forward_f(X, parameters)
			cost = np.squeeze(forward.cost_function(AL, Y))
			grads = backward.backward_function(AL, Y, caches)
			parameters = update_parameters(parameters, grads, learning_rate)
			parameters = prun(parameters, mask_w)
			t.set_description('Retrain %i' % i)
			t.set_postfix(cost=cost)
			t.update(1)

	return parameters, cost

#Print accuracy
def accuracy(parameters):
	Y_prediction_train = predict(parameters, train_x)
	Y_prediction_test = predict(parameters, test_x)
	print("Training set accuracy："  , format(100 - np.mean(np.abs(Y_prediction_train - train_y)) * 100) ,"%")
	print("Test set accuracy："  , format(100 - np.mean(np.abs(Y_prediction_test - test_y)) * 100) ,"%")

#Print Pruning degree
def degree(parameters):
	n=0
	num=0
	L=len(parameters)//2
	for l in range(1, L):
		N=parameters['W'+str(l)]
		for i in N:
			for v in i:
				num+=1
				if v==0:
					n+=1
	degree=n/num*100
	print("Parameter pruning degree: ", round(degree,3),"%")
	return degree

##load dataset
datas = 'datasets/carvnocar.h5'
train_set_x, train_y, test_set_x, test_y = load_files(datas)
train_x = train_set_x / 255
test_x = test_set_x / 255

##load parameters
f_parameters = 'datasets/parameters.npy'
parameters = np.load(f_parameters, allow_pickle='TRUE').item()

L = len(parameters)//2 

print("Original parameters: ")
accuracy(parameters)

def acc0(a):
	n=0
	for i in a:
		for j in i:
			if j == 0:
				n+=1
	return n

def array0(a):
	b=[]
	if acc0(a)>1:
		b.append(0)
	for i in a:
		for j in i:
			if j != 0:
				b.append(j)
	return b

prun_parameter = np.load(f_parameters, allow_pickle='TRUE').item()
#Hyper-parameters
h_threshold=5
delta=0.1
learning_rate=0.05
num_iterations=220

degrees=[]
costs=[]
for i in range(1, 40):
	#Make mask
	mask_w=[]
	for l in range(1,L):
		a=prun_parameter['W'+str(l)]
		b=array0(a)
		threshold=np.percentile(np.abs(b), h_threshold)
		ms=np.abs(a)>threshold
		if i>1:
			ms=np.multiply(ms,mask_w_l[l-1])# Multiply by the mask matrix of the previous step
		mask_w.append(ms)
		# print("threshold "+str(l)+": "+str(threshold))# print threshold
	mask_w_l=mask_w# Save the mask matrix of the previous step
	#Pruning parameters
	prun_parameter=prun(prun_parameter, mask_w)#parameters pruning
	print("\n "+str(i)+" Pruning parameters: ")
	n=degree(prun_parameter)
	degrees.append(n)
	accuracy(prun_parameter)
	#Retrain parameters
	retrain_parameters, cost = retrain(prun_parameter, train_x, train_y, learning_rate, num_iterations)
	costs.append(cost)
	print("\nPruning and retrain parameters: ")
	accuracy(retrain_parameters)
	np.save('datasets/prun_parameter_1/prun_parameters'+str(i)+'.npy', retrain_parameters)
	#Iterative pruning (Not used during the experiment)
    # h_threshold+=delta*i
	# h_threshold+=5

degree_costs={'degree':degrees,'costs':costs}
np.save('datasets/degree_costs.npy', degree_costs)

Experimental record

不同剪枝度得到的训练至收敛后的cost：

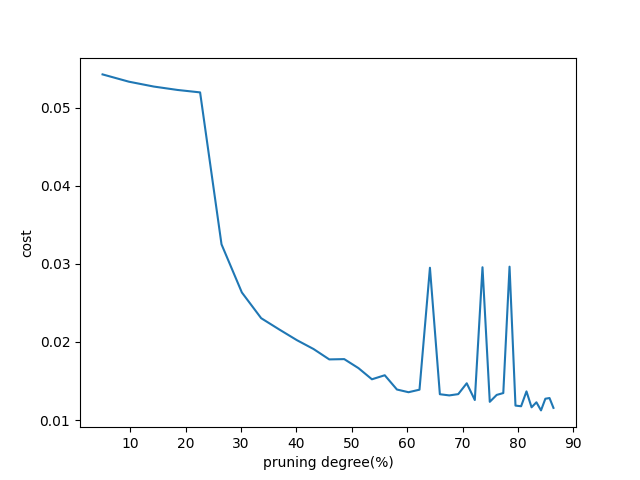
https://s2.loli.net/2023/01/03/tgQWHFR1n8IKXZM.png

使用第三十九次剪枝后重训练得到的参数与原参数进行比对、判断：

Ori parameter:
Parameter pruning degree:  0.0 %
Training set accuracy： 98.89502762430939 %
Test set accuracy： 80.0 %
Pruned parameter:
Parameter pruning degree:  86.406 %
Training set accuracy： 99.4475138121547 %
Test set accuracy： 80.0 %

No pruning 的原W1参数：

[[ 0.17652197 -0.06106679 -0.07412075 ... -0.14664018 -0.00927934
   0.06886687]
 [ 0.11185143 -0.06578853 -0.0011025  ...  0.08918518  0.07352842
  -0.00663041]
 [-0.10772029  0.03944582 -0.24708339 ...  0.0550951  -0.03051575
  -0.06339629]
 [-0.05884084  0.20572945  0.03835234 ...  0.16899935  0.02967805
   0.07047436]
 [ 0.04006457 -0.03186718  0.00984735 ...  0.01321126 -0.09708557
   0.21907507]]

86.406%pruning后的W1参数：

[[ 0.18168446  0.          0.         ...  0.          0.
   0.        ]
 [ 0.          0.          0.         ...  0.          0.
   0.        ]
 [-0.         -0.         -0.25039574 ... -0.         -0.
  -0.        ]
 [ 0.          0.20658655  0.         ...  0.16506836  0.
   0.        ]
 [-0.         -0.         -0.         ... -0.         -0.
   0.23942507]]

原参数对测试图片进行预测：

https://s2.loli.net/2023/01/03/4YToAjPKh5wO9kH.png

Accuracy: 26/27

剪枝后[86.406%]：

https://s2.loli.net/2023/01/03/UQH7gkdM3Ronm5X.png

Accuracy: 25/27

修改→第一版的实验代码中验证模型的部分对数据集没用进行归一化处理，结果出现严重偏差，需要加上归一化

# AI # TinyML
使用STM32CubeMX生成的Makefile工程中使用printf函数在串口打印输出的问题 上一篇
多路信号发生器的Multisim仿真实现 下一篇
已运行:
浏览数: 次 | 访客数: 人